(Written by Nicholas Torres)
An important aspect of conducting NMR analysis is finding two time-constants: T1 and T2. The T1 constant represents the longitudinal relaxation time or how long it will take for a proton that has been energized by a radiofrequency (RF) pulse to go back to realign with the magnetic field, whereas the constant T2 or transversal relaxation time tells us roughly how long it will take for a proton that has been struck with a 90° RF pulse to dephase from its neighboring protons due to different local magnetic environments. It is important to stress the fact that these constants are not the exact times it will take for these processes to happen, simply a representation of how fast the process goes.
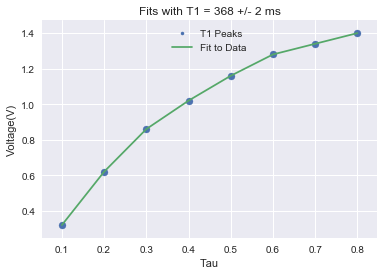
Both T1 and T2 are mathematically represented by these exponential functions: $V= V_0(1-e^{(-\tau/T_1)})$ and $V= V_0e^{(-t/T_2 )}$, where $V$ and $V_0$ are the voltage we expect to measure with our TeachSpin setup. For T1, we use a relaxation recovery sequence (180° pulse-$\tau$-90° pulse) and measure the voltage peak after the 90° pulse for different $\tau$ times. For T2, we use a CPMG sequence and take the voltage peak of the Hahn spin echoes. (The CPMG sequence using the Hahn spin echo to get rid of decoherence due to inhomogeneity of the external magnetic field, as well as changes the phases of the pulses to correct for pulse error.)
Being familiar with these constants is extremely advantageous for developing an MR image, for they provide special contrasting capabilities. For the purposes of the research the Sarah Lawrence Physics Department, we performed NMR analyses on zebrafish because discovering more about their biological makeup can elucidate important facts concerning neurodevelopmental diseases.
In order to collect T1 and T2 data, we utilized the oscilloscope and processed the data using Python. Below is our Python code for the data analysis: A Sample of T2 Data Analysis Python Script
samplingRate = 2500
tau = 0.01
numEchoes = 20
fullfilename = "zebra fish middle body sample" + '.csv'
data = np.loadtxt(fullfilename,delimiter = ',')
plt.plot(data[:,0], data[:,1])
x2=len(data)
maxNum1=max(data[0:x2,1])
count=0
while data[0+count,1] != maxNum1:
count +=1
count +=1
firstPeak=0+count
print(firstPeak)
#Finds first peak value in Hahn Echo
firstPeak = 0
interval=int(2*tau*samplingRate)
print(interval)
#If we know tau, then interval = 2*tau*samplingRate
echoPeaks = [data[interval*j+firstPeak,1] for j in range(numEchoes)]
tEchoes = [data[interval*j+firstPeak,0] for j in range(numEchoes)]
plt.scatter(tEchoes,echoPeaks)
from scipy.optimize import curve_fit
def fitfunc(x, p1, p2, p3):
return p1*np.exp(-x/p2) + p3
poptB, pcovB = curve_fit(fitfunc, tEchoes, echoPeaks,p0=(12,0.01, 0.000001))
perrB = np.sqrt(np.diag(pcovB))
poptB
#Prints array with T2 value and error
fitData = [fitfunc(tEchoes[j], poptB[0], poptB[1], poptB[2]) for j in range(numEchoes)]
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.title('Fits with T2 = 44 +/- 4 ms')
plt.plot(tEchoes, echoPeaks,'.', label='Echo Peaks')
plt.plot(tEchoes, fitData, label = 'Fit to Data')
plt.legend(loc='upper center')
plt.show()
#Constructs and shows plot
A Sample of T1 Data Analysis Python Script
def timearray(sampleRate, numPoints):
sampleSpacing = 1./sampleRate
time = np.linspace(sampleSpacing, sampleSpacing*numPoints, numPoints)
return time
def freqarray(sampleRate, numPoints):
sampleSpacing = 1./sampleRate
freq = np.fft.rfftfreq(numPoints,sampleSpacing)
return freq
time = timearray(1e7, 30000)
freq = freqarray(1e7, 30000)
filenums = [17, 18, 19, 20, 21, 22, 23, 24]
#filenums corresponds tot the last two digits of each Excel file and is meant to be editted for each T1 Data Sample
tauValues = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7,0.8]
#tauValues should correspond to the Tau times set by the Pulse Programmer.
maxYValues = []
n = 0
for n in filenums:
fullfilename = 'TEK00' + str(n)+'.csv'
data = np.loadtxt(fullfilename,delimiter = ',')
maxNumForEachDataSet = max(data[:,1])
maxYValues.append(maxNumForEachDataSet)
n = n + 1
#Iterates through our Excel files in a folder and finds peak values for each file
from scipy.optimize import curve_fit
def fitfunc(x, p1, p2, p3):
return p1*np.exp(-x/p2) + p3
poptB, pcovB = curve_fit(fitfunc, tauValues, maxYValues,p0=(12,0.01, 0.000001))
perrB = np.sqrt(np.diag(pcovB))
poptB
#Prints array with T1 value and error
fitData = [fitfunc(tauValues[j], poptB[0], poptB[1], poptB[2]) for j in range(len(filenums))]
plt.scatter(tauValues, maxYValues)
plt.xlabel('Tau')
plt.ylabel('Voltage(V)')
plt.title('Fits with T1 = 37 +/- 2')
plt.plot(tauValues, maxYValues,'.', label='T1 Peaks')
plt.plot(tauValues, maxYValues, label = 'Fit to Data')
plt.legend(loc='upper center')'
#Constucts and shows plots
What follows are the plots, constructed in Python, for our T1 and T2 data analysis:
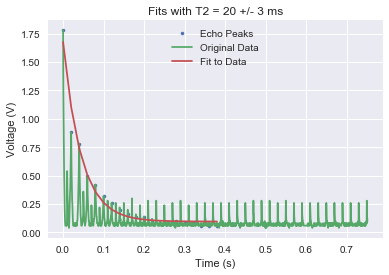
(Note: The extra peaks in the raw T2 data is coming from ringdown from the 180° pulses.)