(Written by Jianlong (Ken) Zhu)

RF Probe

We designed our own RF probe with the aid of a manual, Experimental Pulse NMR: A Nuts and Bolts Approach (Eiichi Fukushima and Stephen B. W. Roeder). Below are some takeaways from the section “V.C.4. Probes” (p.p. 373-385):

• A good coil for RF probe has a large inductance, which is given by the equation: $L = \frac{n^2 a^2}{23a+25b}$ μH, where n is the number of loops, and a and b are the radius of the loop and the length of the coil measured in centimeters.

• The spacing between the turns of the coil should approximately equal to the diameter of the wire.

• The length of the coil should approximately equal to the diameter of the loop.

• “#14 wire is about the smallest that can be recommended for a free standing coil.”

Hand-Made Coil

Our desired resonance frequency is 21 MHz and the capacitance is in the range of 50-1000 pF, the maximum possible inductance for our case is 1.149 μH.

We wanted to fit the coil inside a test tube whose inner radius is 1.3 cm, and also we wanted to keep the length of the coil, b, below 2.5 cm.

Using the maximum L and the desired values for a and b, our Python calculator returned a wire diameter of 0.75mm - way thinner than the recommended #14 wire (1.628mm).

a = 0.56
b = 2.5
L = 1.14877
n = ((23*a+25*b)*L/a**2)**0.5

print('n: '+str(n))
wireWidth = b/(2*n)
print('wire width: ' + str(wireWidth) + ' cm')

Therefore we decided to compromise the inductance and coil length for a thicker wire. We chose a #18 wire (1.024 mm), made L = 1.0 μH, and our Python optimization program returned the values n = 18.52 and b = 3.79 cm.

wireWidth = 0.1024
a = 0.56
n = 0
b=2*n*wireWidth
L = 1

while abs(n-((23*a+25*b)*L/a**2)**0.5)>0.01:
    n+=0.001
    b=2*n*wireWidth
print(n)
print(b)

So the specs of our hand-made coil became:

Wire: AWG #18 Loop radius: a = 0.56 cm Coil length: b = 3.8 cm
Number of loops: n = 18.5 Inductance: L = 1.0 μH

Capacitors

We used a Mathematica calculator to obtain the desired capacitance for our tuning and matching capacitors, 62 pF and 10 pF.

"""
This notebook finds the ideal tuning (C1) and matching (C2) capacitances for a desired resonant frequency given the inductance and resistance of the coil and assuming a 'low resonance' circuit (i.e. matching capacitor in series and tuning capacitor in parallel with the inductor).

"""
Clear[C2, C1, R, L, w, w0, f0, Z, Q];
(* Desired resonance frequency (Hz) *)
f0 := 18.735 10^6;
w0 := 2*Pi*f0; 
(* Inductance of coil (H) *)
L := 1 10^(-6);
(* Resistance of coil (Ohms) *)
R := 1(* Theoretically from 90 cm of AWG-18 copper wire: 0.0210*0.9 *);

Q := w0 L/R;
StringJoin["Q = ", TextString[Q]]

(* Low frequency circuit impedance *)
Z := (I w L + R)/(1 - w^2 C1 L + I w C1 R) + 1/(I w C2);
(* Current thru coil *)
IL := 1/(Z + 50)/(1 - w^2 C1 L + I w C1 R);
(* Find values of w and C2 that maximize current through coil (by
finding the minimum of the inverse curve) *)
FindMinimum[-Abs[IL] /. w -> w0, {C1, 5 10^(-9), 500 10^(-9)}, {C2, 
  5 10^(-9), 500 10^(-9)}]

(* Checks that the above values for C1 and C2 give the expected
impedance *)
StringJoin["{Re[Z], Im[Z]} = ", 
 TextString[{Re[Z], Im[Z]} /. {w -> w0, C1 -> 6.19738 *10^(-11), 
    C2 -> 1.02239*10^(-11)}]]

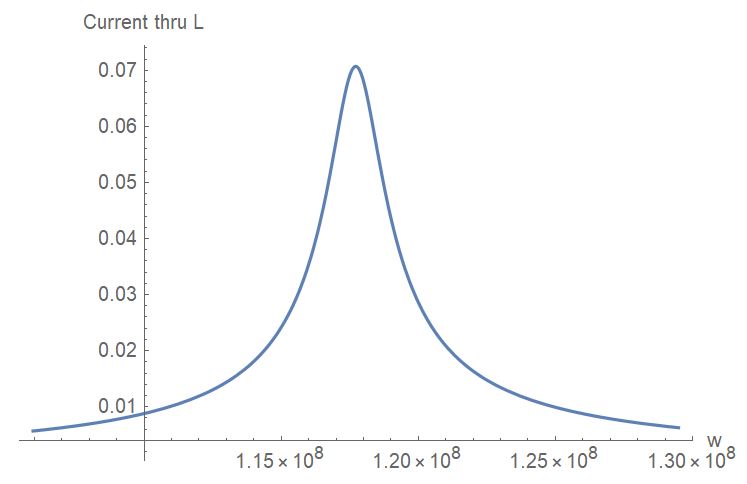
(* Plots resonance peak with matching impedance *)
Plot[Abs[IL] /. {C1 -> 6.19738 *10^(-11), C2 -> 1.02239*10^(-11)}, {w,
   0.90 w0, 1.10 w0}, AxesLabel -> {"w", "Current thru L"}, 
 PlotRange -> All]  

Desired resonance curve

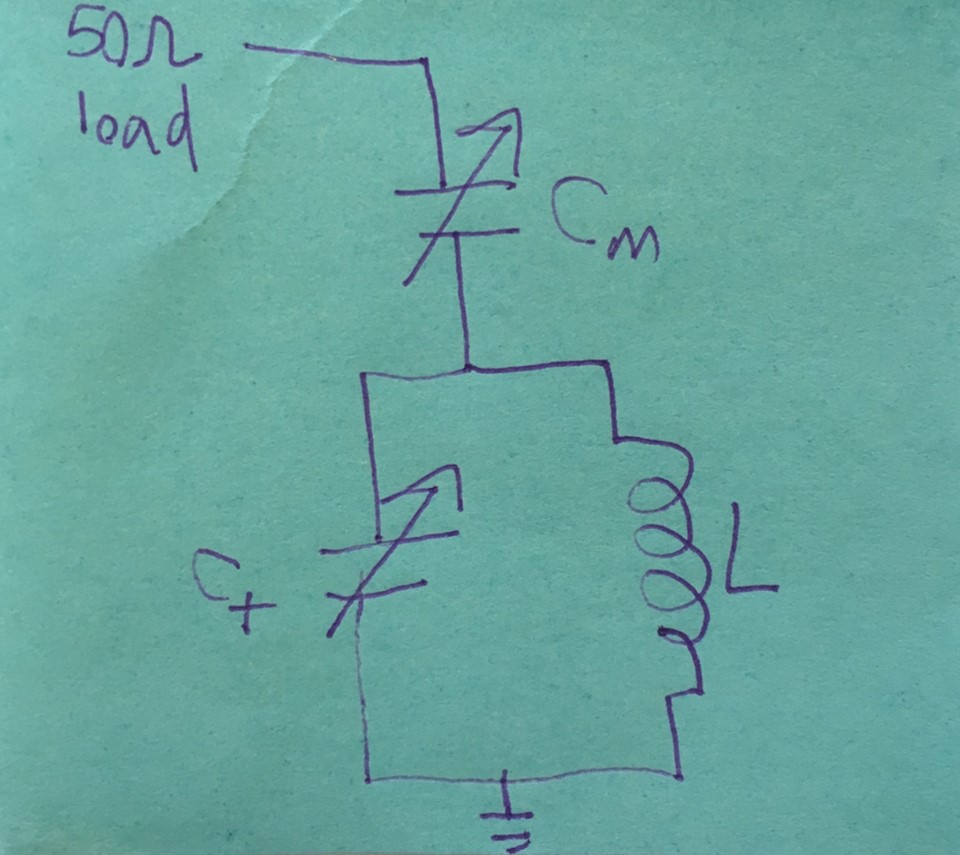
Assembly

The next step was to solder the parts together according to the circuit diagram below:

Product

Similarly, we assembled another RF probe with a factory-made coil whose inductance is 0.36 μH.

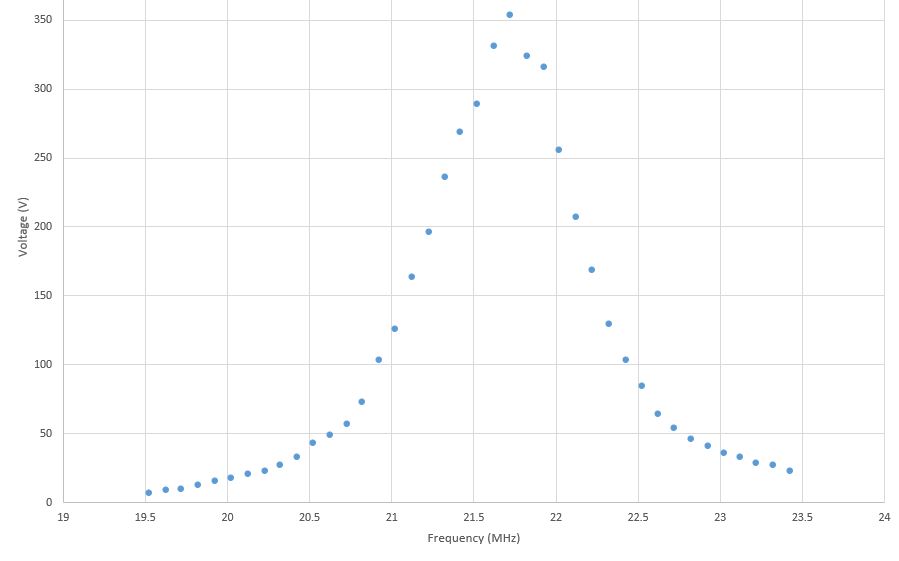
The RF probe with our hand-made coil yielded a quality factor (Q) of 19.75, and below is the resonance curve: