The Computational Beauty of Nature — Spring 2020

Problem Set 2: L-Systems and Fractal Dimension

Due by class time Thursday, February 20

For these exercises, you should write up your solutions either by hand or using a word-processing program such as Word. Handwritten work is acceptable as long as you write neatly and legibly, but you'll lose points if I have to struggle to read your answers.

Reading

• Next week, we will begin our discussion of Chaos, so you should begin reading:

  • Chapter 2 of Complexity: A Guided Tour (pages 15-39)
  • Chapter 10 of The Computational Beauty of Nature (pages 139-158)

Written Exercises

1. Write out your answers to the starred exercises 11, 12, 13, 17, 18, and 20 from the L-system lab worksheet (Lab 2). For exercise 20 (creating your own L-system fractal), include your axiom, rule(s), and other parameter settings, as well as a printout of your screenshot.

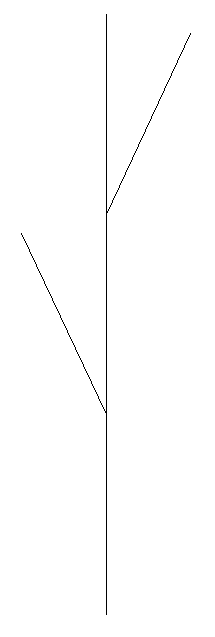
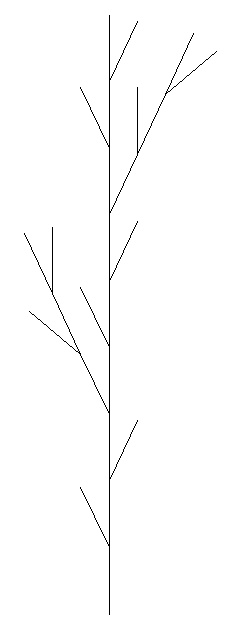
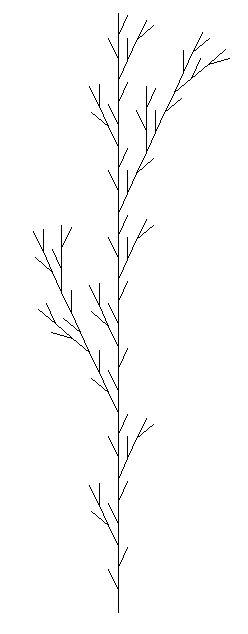
2. What is the fractal dimension of the "Weed 1" L-system fractal shown below? Show how you calculated this. Hint: remember the phrase "N parts scaled by 1/M".

   . . .

3. We can create a two-dimensional analogue of the Cantor set by starting with a square and removing part of its interior, leaving behind four smaller squares at the corners. Continuing this process forever will generate a "2-D Cantor set" fractal, as illustrated below:

   . . .

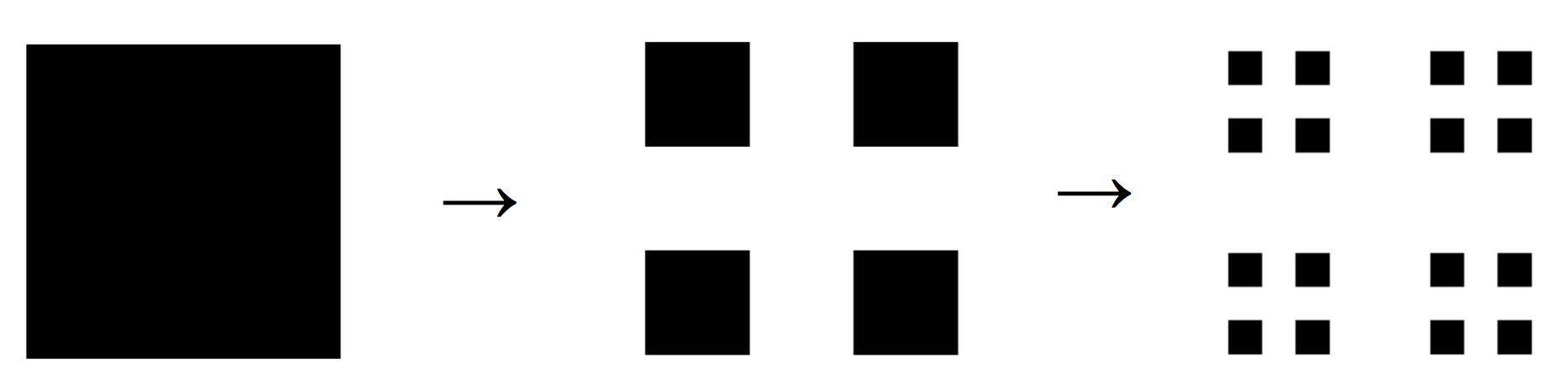   1. What is the fractal dimension of the 2-D Cantor set? Show how you calculated this.

   2. Assuming that the area of the original starting square is 1, give a general formula that can be used to calculate the total remaining area after n steps.

   3. What is the total remaining area of the 2-D Cantor set in the limit (that is, after an infinite number of steps)? Explain your answer clearly.

4. A Menger sponge (shown below on the left) is a 3-dimensional analogue of the Sierpinski carpet (shown in the middle). We start with a solid cube and divide it into 27 smaller sub-cubes, with 9 sub-cubes on each face. We then remove the center sub-cube from each face, along with the sub-cube in the very center of the larger cube, and repeat this process forever. The picture on the right illustrates the first three steps. Calculate the fractal dimension of the Menger sponge, and justify your answer. (Also check out this article for a surprising new view of the Menger sponge.)

5. A Sierpinski tetrahedron (below left) is a 3-dimensional analogue of the Sierpinski triangle (below right), with 3 faces and a base that is an equilateral triangle. Calculate the fractal dimension of the Sierpinski tetrahedron, and justify your answer. Just for fun, here is a Sierpinski tetrahedron made out of LEGOs, and another one in honor of Valentine's Day.