In the simulator, load in the circuit named 2-Way MUX Circuit. This is a simple multiplexor circuit. The two switches on the left are the multiplexor's input lines; the switch at the bottom selects one of these two input lines to be the output of the circuit. With the select switch set to 1, the top input is selected; with select = 0, the bottom input is selected. Test out this circuit until you understand how it works. Draw a truth table showing the circuit's behavior for all possible values of its inputs. Label the columns of your table A (for the top input), B (for the bottom input), SELECT (for the selector switch), and OUT (for the output signal).
What is the total number of logic gates required to build a circuit to
add two 4-digit binary numbers, like the one discussed in class, assuming that
only AND, OR, and NOT gates are used? For this question, assume that a
half-adder is implemented as shown below:
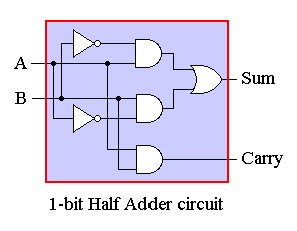
Suppose that we're allowed to use XOR gates, in addition to AND, OR, and NOT gates. What is the total number of logic gates required to build the circuit from question 2 now?
Assuming that a single 1-bit memory circuit requires 7 logic gates (as in the 1-Bit Memory Circuit from Lab 12), what is the total number of logic gates required to implement the RAM memory of the PIPPIN computer, assuming that it can store a maximum of 256 8-bit data values in its memory? Note that this does not include PIPPIN's CPU registers (i.e., the Accumulator, Program Counter, or Instruction Register), or other CPU components such as the ALU.
The logical operator IMPLIES is a formalization of what we mean when we say "if ... then". In particular, A IMPLIES B is false only in the case when A is true and B is false. For example, "If it is sunny, then Sally is on the golf course" is a false statement only in the case that it's sunny and Sally isn't on the golf course. Notice that according to this definition, if A is false, then the truth or falsity of B is irrelevant; A IMPLIES B is automatically true. For example, "If pigs can fly, then I'm Britney Spears" is a true statement (because pigs can't fly). Find a way to express IMPLIES using some combination of ANDs, ORs, and NOTs. Build the appropriate circuit in the circuit simulator, and test it out to make sure it works. Write out your logical expression on paper, and draw the final circuit.
Draw a circuit that implements the following logical expression:
A AND (NOT (A OR (NOT B)))
Show that it would be a waste of time to actually build this circuit, by finding the output of this expression for all possible values of A and B. Do this by writing out the complete truth table for the expression.