Developed by Pentti Kanerva
How are concepts related to one another?
- Any one concept is unrelated to most of the rest, but for any two
unrelated concepts we can always find an intermediate concept that is
related to each of the first two.
- Concepts can be linked in many ways
- Memory items in SDM are arranged so that most items are
unrelated to one another but most pairs of items can be linked by just
one or two intermediate items.
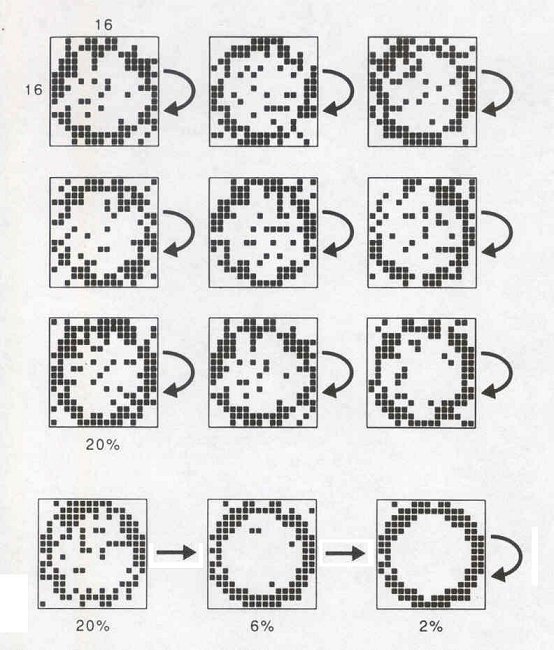
How do we know when we know?
- When shown a face, we either:
- immediately recognize the person
- are uncertain, but have a sense as to how close we are to knowing
- immediately know that we've never seen them before
- We don't scan through a sequence of stored patterns;
instead we reach for the information directly.
- In SDM, patterns serve as addresses into memory
- Like a giant "hash table" with an identity hashing function
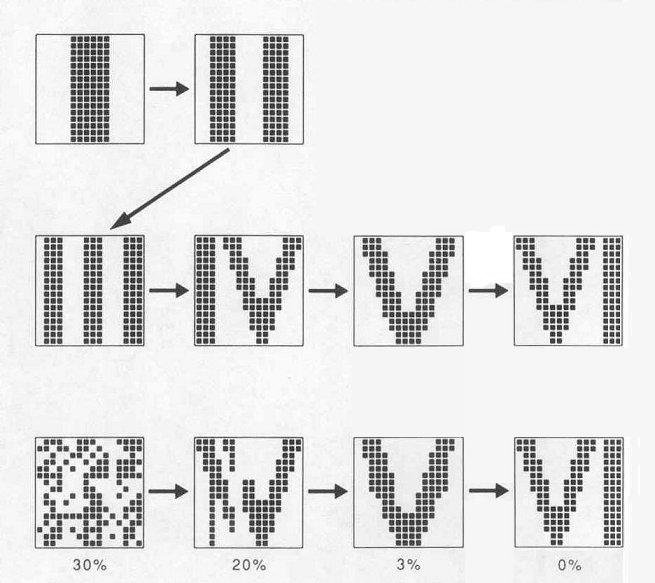
Sequences
- Experience is stored as temporal sequences that accumulate over time
- One sequence item helps to retrieve the next
- saying the alphabet forward versus backward
- piano rehearsal
- Sequences can be retrieved using any part of the sequence as a cue
- SDM model supports both random access and sequential
retrieval in a natural way
Human memory is a function of brain organization
- SDM is constructed from neuronlike components in a
physiologically plausible way.
- Neurons are used as address decoders for each location in the memory.
- Architecture is massively parallel.
- Architecture is strikingly similar to structures found in the
cerebellum. This may not be a coincidence.
SDM Model
- Memory items are represented by N-bit patterns, where N is
typically in the range 100-10,000 (or more).
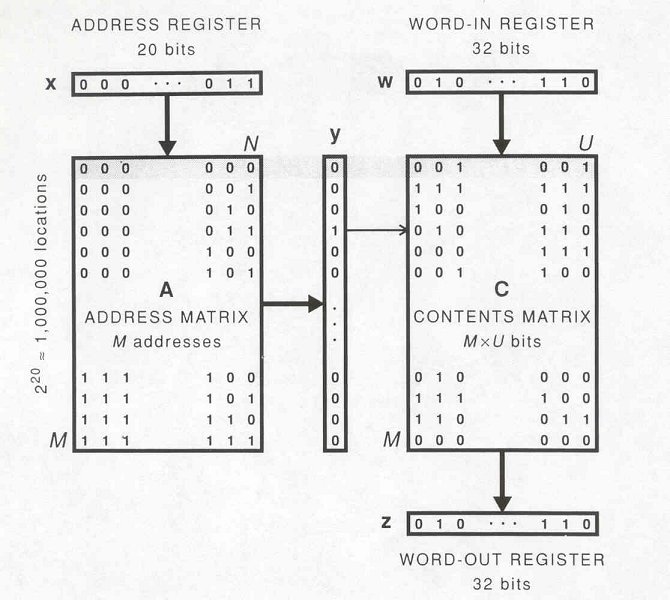
- Items stored in the memory are addresses to the memory.
- Sequences are stored as pointer chains.
- Size of address space is 2N for N-bit words.
- Address space consists of the corners of a N-dimensional hypercube:
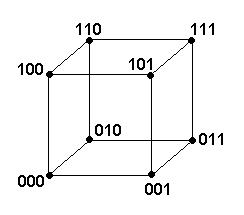
- Distance between two addresses is the Hamming distance (# of
mismatched 0's or 1's):
0010010101010001
0000000101011111
Hamming distance = 5
- Sphere analogy: addresses are like points on the surface
of a 3-D sphere. Pole opposite address x corresponds to the
complement of x. Points on the equator correspond to addresses
at distance N/2 from x.
- Any address can be considered the "origin" (choose 000...0 for
convenience).
Distribution of address space
- # of addresses that are D bits from the origin = # of addresses
containing exactly D 1's.
- (N choose D) addresses at distance D.
- Distribution of space follows binomial distribution
(with mean N/2, variance N/4).
- Most of the space is nearly orthogonal to any given address (the
larger N is, the more pronounced is this effect).
- In terms of the sphere analogy, almost all of the space lies near the
equator.
- Example: with N = 1000, a circular region of radius 425 bits centered on
x encloses only about a millionth of the space.
| Radius of circle centered on x |
Portion of space enclosed |
| 405 bits (41% of N) |
0.000000001 |
| 425 bits (42%) |
0.000001 |
| 441 bits (44%) |
0.0001 |
| 451 bits (45%) |
0.001 |
| 463 bits (46%) |
0.01 |
| 480 bits (48%) |
0.1 |
| 489 bits (49%) |
0.25 |
| 500 bits (50%) |
0.5 |
| 511 bits (51%) |
0.75 |
| 520 bits (52%) |
0.9 |
| 575 bits (58%) |
0.999999 |
- Almost all points are unrelated (lie at about distance N/2), but any two
points at distance N/4 are extremely similar (only an exceedingly tiny
fraction of the space is closer)
- Distribution of a circle centered on x with radius D:

- Distribution of the intersection of two circles of size N/10000:
Distance between centers
(relative to circle diameter) |
Relative size of overlap |
| 0.0 |
1.0 |
| 0.05 |
0.37 |
| 0.1 |
0.19 |
| 0.2 |
0.05 |
| 0.3 |
0.01 |
| 0.5 |
0.0001 |
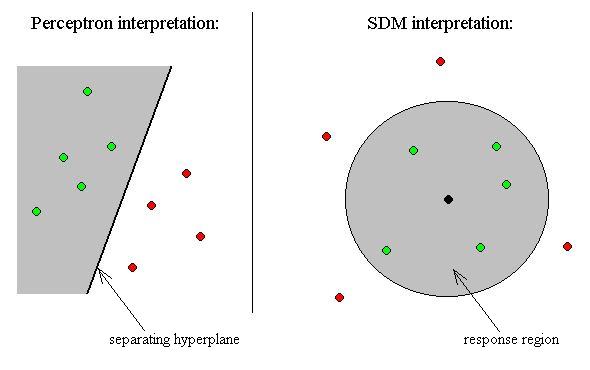
- A concept or memory item can be thought of as a region centered on an
address x.
Neurons as address decoders
Sparse, Distributed Storage
- With N = 100-10,000, no way to construct 2N physical memory
locations (only ~ 236 neurons in CNS; a century has <
232 seconds).
- Storage locations and addresses are given from the start ("hard
locations"); only contents of locations are modifiable.
- Storage locations are very few compared to 2N.
- Storage locations are distributed randomly throughout address space.
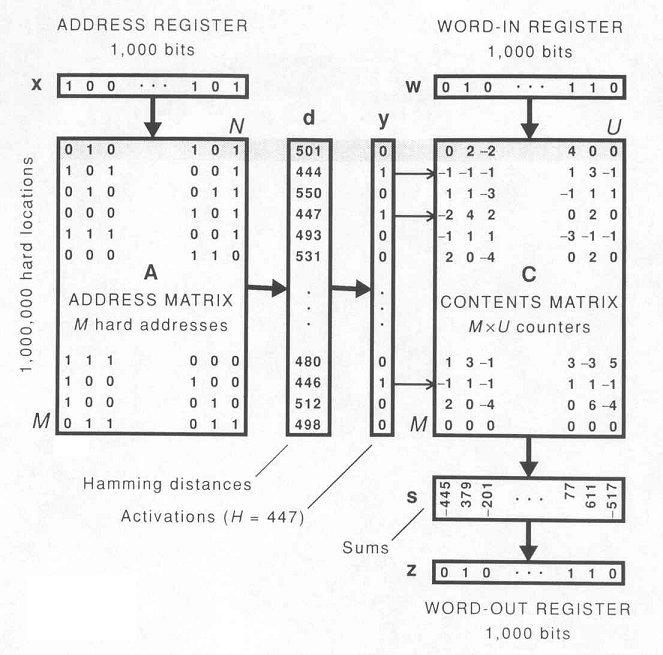
- Example: With 1000-bit words, randomly choose 1,000,000 hard locations out of a
possible 21000.
- Memory is exceedingly sparse: only
2-980 of the address space is assigned to physical
locations.
- Each hard location represents about a millionth of the space
(2980 addresses), on average.
- Average distance to nearest hard location is about 424 bits.
- Only once in about 10,000 is the nearest location closer than 400 bits.
- Writing y at address x stores a copy of y in each of
the hard locations within x's response region.
- Reading from address x retrieves the contents of all hard locations
within x's response region and averages them together.
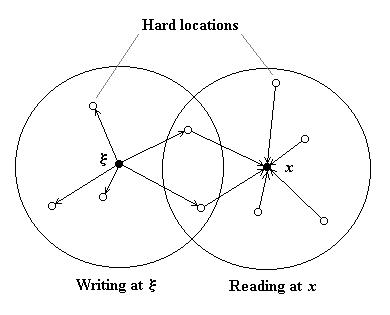
- Average is computed by applying the majority rule to each bit
position, independently of the others.
- Each hard location contains N counters that record # of excess 1's for
each bit position.
Conventional Random-Access Memory Architecture