Genetic Algorithms
Use ideas from biological evolution to evolve
solutions to problems automatically, rather than designing them by hand.
Genetic algorithms recombine candidate solutions
to form new candidates
(Reference: "Genetic Algorithms", John H. Holland, Scientific
American, July 1992.)
Main Components of a Genetic Algorithm
-
Encoding of candidate solutions in some formal representation,
such as bit strings ("chromosomes") .
-
A fitness function that maps candidate solutions to
real numbers.
-
The fitness function defines a fitness landscape over
the search space (similar to error landscape over weight space for neural
networks)
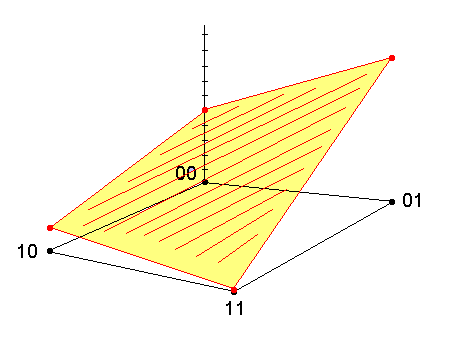
f (00) --> 0.5
f (01) --> 0.9
f (10) --> 0.1
f (11) --> 0.0
A population of candidate solutions
-
A set of genetic operators for transforming candidate
solutions into new candidate solutions.
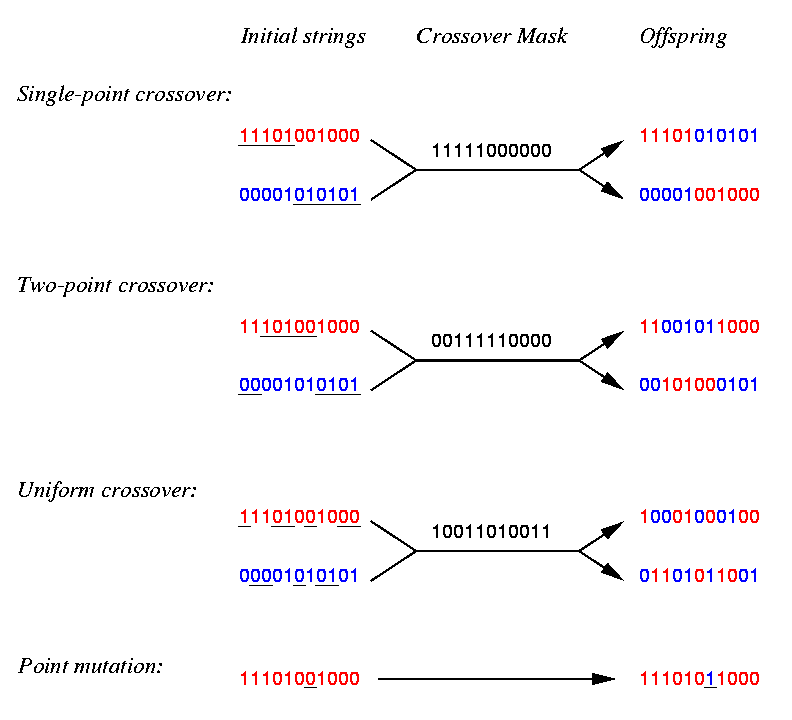
Genetic Operators
-
selection - select chromosomes for inclusion in the
next generation as a probabilistic function of fitness
-
crossover - combine two chromosomes to produce new
chromosomes for inclusion in the next generation (akin to sexual recombination
in nature)
-
mutation - modify components of a chromosome (alleles)
with some probability
Simple Genetic Algorithm
1. Generate random population of N L-bit chromosomes
2. Calculate fitness f (x) of each chromosome
in population
3. Repeat until N offspring have been created:
-
Select a pair of chromosomes from the current population
as a probabilistic function of fitness
-
With probability pc,
perform crossover on chromosomes
-
Mutate each bit of offspring chromosomes with probability
pm
-
Add offspring to the new population
4. Replace current population with new population
5. Go to step 2
Schemas
A schema is a template that represents a set of bit
strings
**1**0*
--> { 1110000,
0010001,
0111001,
0010000,
...
}
Every schema s has an estimated average fitness
f(s), determined by the fitness function and the current instances
of s in the population
Schema Theorem:
Et+1
> k · [ f(s) / f(pop) ]
· Et
(John Holland, 1975)
where
-
Et
is the expected number of instances of schema s in the population
at time t
-
f(s) is the estimated average fitness of schema s
-
f(pop) is the average fitness of all strings in the
population
-
k > 0 is a constant that depends on schema s
Schema s receives exponentially increasing or decreasing
numbers of instances in the population, depending on ratio f(s)
/ f(pop)
Above average schemas will tend to spread through population,
below-average schemas will tend to disappear
This happens simultaneously for all schemas present
in the population ("implicit parallelism")
Example
-
Fitness function f (x) = number of 1 bits in
chromosome
-
Crossover probability pc
= 0.7
-
Mutation probability pm
= 0.001
| Chromosome |
Fitness |
| A: 00000110 |
2 |
| B: 11101110 |
6 |
| C: 00100000 |
1 |
| D: 00110100 |
3 |
Average fitness of population = 12/4 = 3.0

1. B and C selected, crossover not performed
2. B mutated
B: 11101110
----> B': 01101110
3. B and D selected, crossover performed
B: 11101110
E: 10110100
---->
D: 00110100
F: 01101110
4. E mutated
E: 10110100
----> E': 10110000
New population:
| Chromosome |
Fitness |
| B': 01101110 |
5 |
| C: 00100000 |
1 |
| E': 10110000 |
3 |
| F: 01101110 |
5 |
Best-fit string from previous population
lost, but...
Average fitness of population now
14/4 = 3.5
Evolving Neural Network Architectures
- Many ways to encode a neural network as a chromosome
- Specificity of genotype->phenotype mapping can vary over a
wide range:
- Chromosome encodes each weight value directly
- Chromosome encodes constraints for each weight value (e.g., learnable,
fixed, positive, negative)
- Chromosome encodes connectivity between groups of units (e.g.,
layers, modules)
- Chromosome encodes a genetic "blueprint" that must be translated into a
network via a developmental process (which itself may be encoded on the
chromosome)
- Example: Miller, Todd, and Hegde evolved network architectures for
solving XOR, 4-Quadrant, and Copying problems
- Chromosome specified constraints (learnable vs. fixed) for each weight and
bias of the network
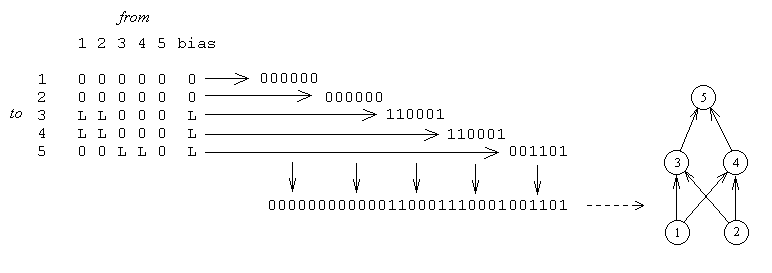
- Fitness determined by network's performance on the training task after
a fixed number of epochs of backprop with randomly-initialized weights
- Results: GA tended to find asymmetric, non-uniform architectures that
worked well
Evolving a Neural Controller for a Simulated Walking Insect
Work by Randy Beer at Case Western Reserve
Reference: Beer, R.D. (1995), "A dynamical systems
perspective on autonomous agents", Artificial Intelligence 72, 173-215.
-
simulated insect with six legs ("hexapod")
-
each leg controlled by three effectors ("muscles")
-
leg position (up or down)
-
forward torque
-
backward torque
-
at least three legs must be down simultaneously to maintain
balance
-
center of gravity must lie within polygon spanned by supporting
feet
-
each leg has a sensor that measures its angle relative to
the body axis
-
genetic algorithm was used to evolve a neural network for
controlling the insect
-
each leg controlled by a fully-recurrent neural network with
five units
-
continuous-valued units with sigmoid activation functions
-
each unit received input from the leg's angle sensor
-
three units controlled the leg's effectors
-
activation of foot unit determined whether foot was up or
down ( > 0.5 ==> up)
-
activations of forward/backward swing units determined amount
of torque applied
-
each leg controller network consisted of 40 parameters:
-
25 recurrent weights
-
5 angle-sensor weights
-
5 biases
-
5 time constants (determined slope of sigmoid)
-
complete architecture consisted of six leg-controller
networks with identical weights
-
ipsilateral (side) connection weights were identical on both
sides
-
contralateral connection weights (connecting both sides)
were identical for all leg pairs
-
total of 50 independent parameters to be optimized
Genetic Algorithm
-
each network parameter encoded as four bits
-
fitness-proportionate selection (roulette wheel)
-
crossover rate 0.6
-
mutation rate 0.0001
-
population size 500
-
fitness function: distance insect moved forward in a fixed
amount of time
-
evolved for 100 generations
Problem Requirements
-
network has to generate motor signals that allow insect to
walk
-
insect has to maintain center of gravity
Results
-
early networks stood on all six feet and pushed until they
fell
-
other networks could move forward but lost their balance
-
later networks could move forward while maintaining stability
-
some evolved a tripod gait (front and back legs on
one side synchronized with opposite middle leg)
-
tripod gait is common among fast-walking insects in nature
-
no learning algorithm involved -- GA determined neural network
weights
-
very computationally intensive
-
much knowledge is designed in from the start
-
body shape
-
sensors
-
neural network architecture
-
training a fully-recurrent neural network is a hard task,
but the GA performed well






