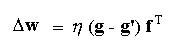
The delta rule (or Widrow-Hoff or Adaline rule) updates the weights of the network based on the amount of error observed at the output layer. The outer product form of the rule is shown below.
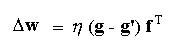
The learning rate (eta) is usually a small constant between zero and one. A trick sometimes used is to let eta be proportional to 1/n, where n corresponds to the nth learning trial. Use of a decreasing learning rate is sometimes called tapering. (Don't try tapering at first -- the system will work fine without using it, as long as you are not storing very many associations.) If eta = 1 / fTf (i.e., the reciprocal of the square of the length of f), the system will respond perfectly immediately after adjusting the weights for the association f -> g. (Do you see why this should be the case?)
Some care has to be taken with the value of eta. If eta is too large, the system will oscillate and may diverge (try it and see). Learning will overcorrect, and may actually increase the error. If eta is too small the system will take a very long time to converge to a correct answer. If eta is constant, W may oscillate around the "best" matrix, without ever converging to a final value.
Suppose we have a set of associations. Suppose we present pairs from this set to the learning system at random. If eta is relatively large (on the order of 1 / fTf), the association will be perfect (or nearly so) for the immediately past pair. It will be less good if a pair has not been presented recently, because the corrections to later pairs may have corrupted the association between earlier pairs. This error correction system displays some of the properties of a short term memory, in that it gives very good responses to the immedate past associations, and then gets progressively worse for more temporally distant associations.
Your task for this part of the assignment is to repeat your studies of the linear associator from the last assignment using the delta rule learning procedure described above.
A good way to proceed is to keep a set of associations in a pair of arrays and then pick pairs at random, associating them using the error correction rule. Add the resulting matrix of weight corrections to the developing weight matrix. Keep going until done. Part of the lore of error correcting models is that the pairs to be learned must be presented in random order. Otherwise, strong sequential dependencies will be built into the matrix. This behavior might be an interesting thing to investigate systematically.
Things to look for include:
Now test your associator on some real-world data. The file cancer.in (also available on turing and pccs in /cs/cs152/data) contains actual clinical data for breast cancer presence based on 9 measured variables. This file follows a set format:
Modify your program so that it can read in data patterns from a file. Then test your network by training it with the delta rule on some subset of the breast cancer data, until the error measure drops below some acceptable threshold. How well is it able to classify the training data? Next, test the network's generalization ability by testing it on patterns from the data set that were not included in the training data. Does it still produce correct classifications for these novel patterns? Experiment with different sizes of training/testing sets, different termination thresholds, and different learning rates.
Two smaller data files are also available for testing your network: nand.in and xor.in. How long does it take your network to converge on the nand patterns? What about xor?