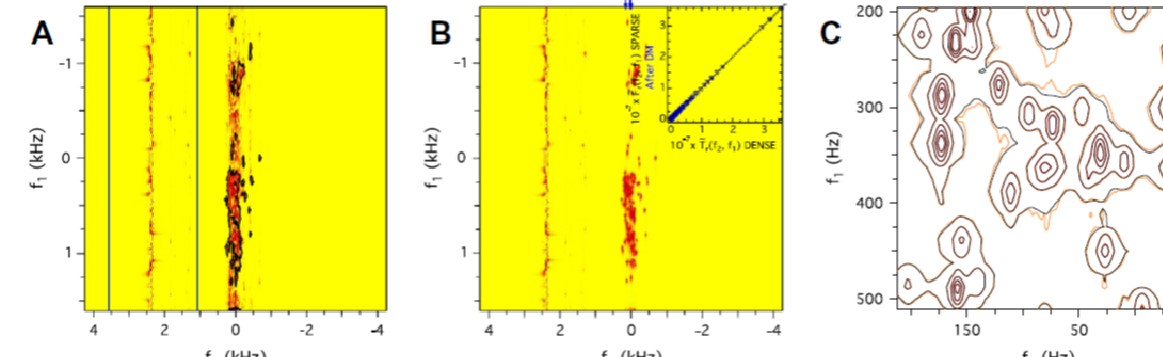

Techniques that accelerate data acquisition without sacrificing the advantages of fast Fourier transform (FFT) reconstruction could benefit a wide variety of magnetic resonance experiments. Here we discuss an approach for reconstructing multidimensional nuclear magnetic resonance (NMR) spectra and MR images from sparsely-sampled time domain data, by way of iterated maps. This method exploits the computational speed of the FFT algorithm and is done in a deterministic way, by reformulating any a priori knowledge or constraints into projections, and then iterating. In this paper we explain the motivation behind this approach, the formulation of the specific projections, the benefits of using a ‘QUasi-Even Sampling, plus jiTter’ (QUEST) sampling schedule, and various methods for handling noise. Applying the iterated maps method to real 2D NMR and 3D MRI of solids data, we show that it is flexible and robust enough to handle large data sets with significant noise and artifacts.