As part of my close reading of Soltner and Blumler’s 2010 article “Dipolar Halbach Magnet Stacks Made from Identically Shaped Permanent Magnets for Magnetic Resonance”, I noted using the dipole approximation for each magnet in order to optimize magnet position to take into account inhomogeneities in the magnetic moments of the magnets used in the Mandhala (see ‘Variation of Magnet Properties’ section of article).
The article creates a ‘cost function’ that measured the deviation of the magnetic field at the center of the Mandhala from what one would get if all the magnets were exactly identical with magnetic moments equal to the mean of the magnets being used. This ‘cost function’ approximates that all the magnets contribute to the field as ideal magnetic dipoles, which works well in the far-field case. One then tries all possible permutation of magnets in each of the available spots, and saves the configuration with the minimal cost function.
Note: Our implementation of this method finds the configuration where the magnetic field at the center is close to the average magnetic field one would expect from the given magnets. This condition can be met by having a symmetric gradient of the magnetic field in the 2D plane (e.g. higher fields on one side, lower fields on the other, the center field being exactly average). Looking at our mapping of the resulting magnetic fields, this might have occurred.
Figure of the magnetic field mappings for the taller Mandhala with center Mandhala (both optimized using the method described above):
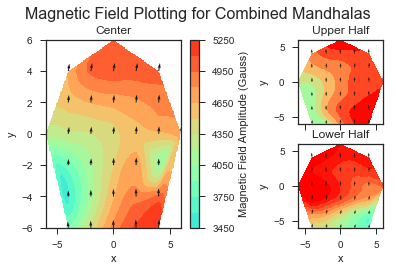
For the future, we might explore adjusting the cost function to sum (or square-root the sum of the squares?) the field deviation over more points than just the central point (perhaps take a good sampling of points over the imaging volume of interest).
We did this optimization separately for the tall Mandhala (using 2” tall magnets) and a new center Mandhala (same design as in 2017).
We typically bought 10 magnets, measured the magnetic flux density at the surface of the north pole, and then found which permutation of 8 magnets from these 10 would result in the most homogeneous field using the Python code below. (In reality, we measured the magnetic flux density of the north face at different ends of the magnet and took the average for the program. However we noted which end was ‘stronger’ and oriented the magnets so that all the stronger ends were at one end of the cylinder, in hopes that perhaps this might provide some sort of gradient along the axis of the cylinder that can be utilized for imaging.)
The code shows choosing 8 magnets from 9 (instead of our usual 10) because in this particular case we had a tragic incident where many magnet lives were lost…
import numpy as np
from itertools import permutations
N = 8 #Input number of spaces in NMR Mandhala to optimize
numMagnets = 9 #Input number of magnets to choose from
# Input surface magnetic field values
#for each of the N magnets to be placed in Mandhala
magnets = np.empty(numMagnets)
magnets[0] = 4145.7
magnets[1] = 4046.5
magnets[2] = 3888
magnets[3] = 4084.8
magnets[4] = 4475.1
magnets[5] = 4183.9
magnets[6] = 4217.5
magnets[7] = 4385.7
magnets[8] = 4253.1
alpha = np.array([n*2*np.pi/N for n in range(N)])
beta = 2*alpha
a = np.zeros(N)
b = np.sin(alpha)
c = np.cos(alpha)
n = np.vstack([a, b, c]).T
p_min = np.zeros(N)
val_min = np.Infinity
for p in permutations(range(numMagnets),N):
m = magnets.take(p)
m0 = np.mean(m)
delta = m - m0
delmV = np.array([delta[i]*np.array([0, np.sin(beta[i]), np.cos(beta[i])]) for i in range(N)])
costV = np.sum(np.array([3*(np.dot(delmV[i], n[i]) * n[i]) - delmV[i] for i in range(N)]),0)
val = np.linalg.norm(costV)
if val < val_min:
val_min = val
p_min = p
print("Minimum Value:", val_min)
print("Permutation corresponding to the minimum value:", p_min)
print(magnets.take(p_min))
print("Average magnetic field value:", np.mean(magnets.take(p_min)))