Principles of Programming Languages — Homework 7

Due by class time Thursday, October 3

Reading

Review the code examples from class today. If you like, you can read more about let-expressions here.

Exercises

  1. Here is our meaning function for infix expressions, which we wrote in class:

    (define meaning
  (lambda (exp)
    (cond
      [(number? exp) exp]
      [(symbol? exp) (error "unknown value for variable:" exp)]
      [(and (list? exp) (= (length exp) 3))
       (cond
         [(eq? (operator exp) '+)
          (+ (meaning (left-side exp)) (meaning (right-side exp)))]
         [(eq? (operator exp) '-)
          (- (meaning (left-side exp)) (meaning (right-side exp)))]
         [(eq? (operator exp) '*)
          (* (meaning (left-side exp)) (meaning (right-side exp)))]
         [(eq? (operator exp) '/)
          (/ (meaning (left-side exp)) (meaning (right-side exp)))]
         [else (error "unknown operator:" (operator exp))])]
      [else (error "invalid infix expression:" exp)])))

    Rewrite this function using a let-expression to make the code more readable, by giving the result of the recursive call (meaning (left-side exp)) the name value1 and the result of the recursive call on the right side the name value2. Hint: your let-expression should go immediately before the inner cond.

  2. The good old quadratic formula from high school math is shown below:

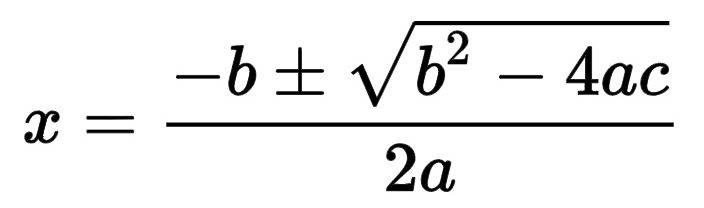
    This formula is used to compute the value of x in the equation ax2 + bx + c = 0. There are always two possible values of x (called "roots") that will satisfy the equation, one calculated using addition in place of the ± symbol and the other using subtraction. Here is a function that will compute the two roots of the equation, given input values a, b, and c, and return them in a single list: 

    (define quadratic
  (lambda (a b c)
    (list
      (/ (+ (- b) (sqrt (- (* b b) (* 4 a c)))) (* 2 a))
      (/ (- (- b) (sqrt (- (* b b) (* 4 a c)))) (* 2 a)))))
    Rewrite this function using a let-expression to avoid computing the square root of b2 − 4ac twice. Use another let-expression to give the names x1 and x2 to the individual roots, and return the final result as (list x1 x2). Examples: 
    (quadratic 1 3 2)    →  (-1 -2)
(quadratic -2 -4 0)  →  (-2 0)
(quadratic 4 -5 1)   →  (1 1/4)

  3. Write the function (extend1 var val env) that takes a variable var, a value val, and an environment env as input, and returns a new environment containing a new binding (var val), along with all of the other bindings from env. Hint: there is no need for this function to be recursive. Example:

    (define env1 '((a 1) (b 2) (c 3)))

(extend1 'z 50 env1)  →  ((z 50) (a 1) (b 2) (c 3))

Turning in Your Homework