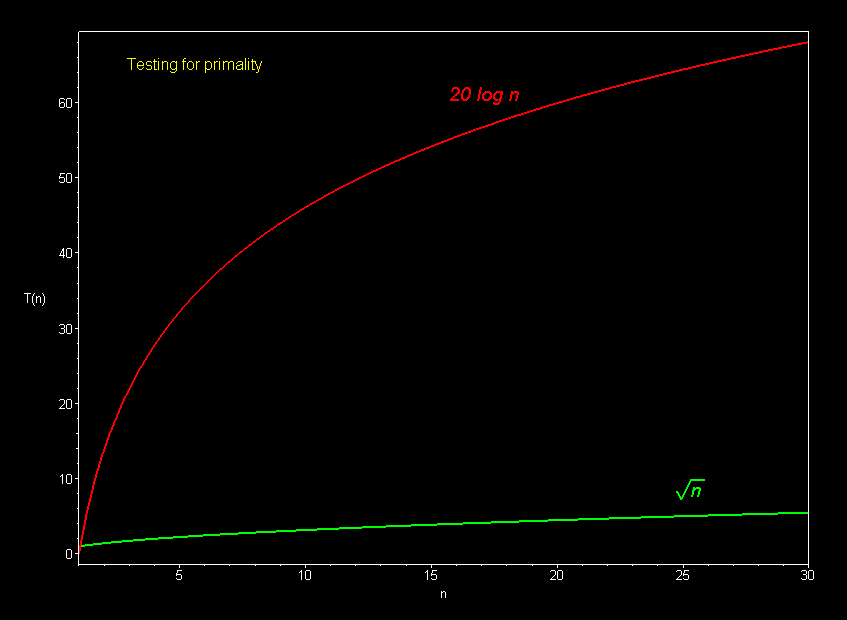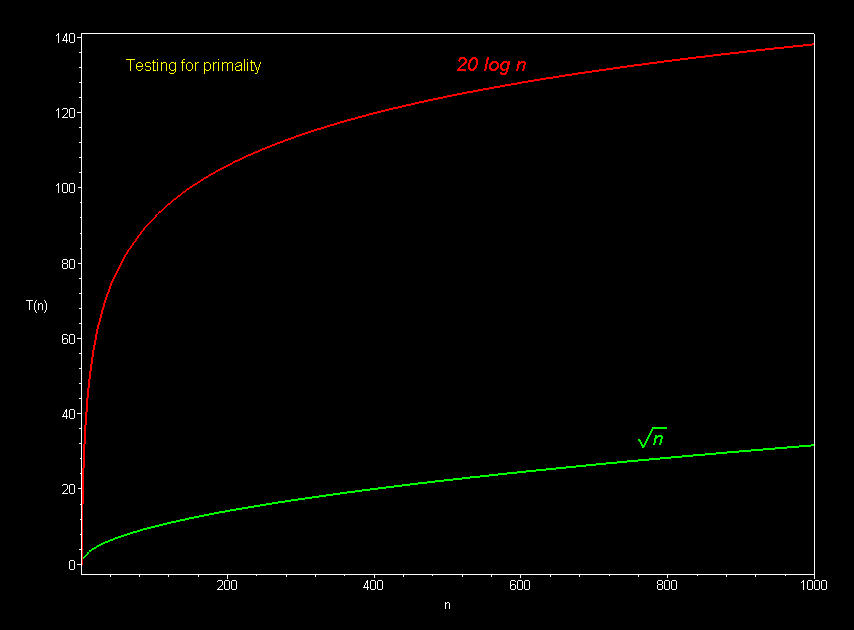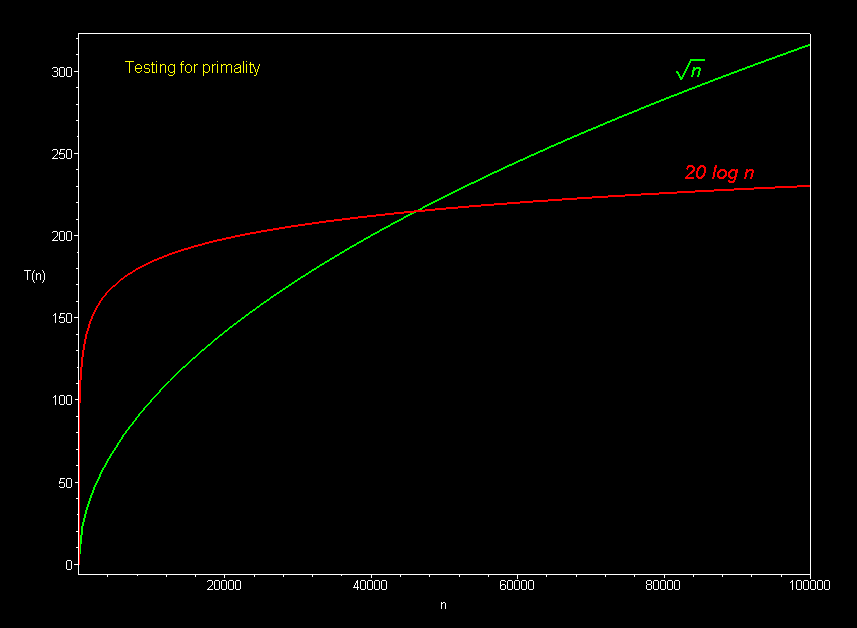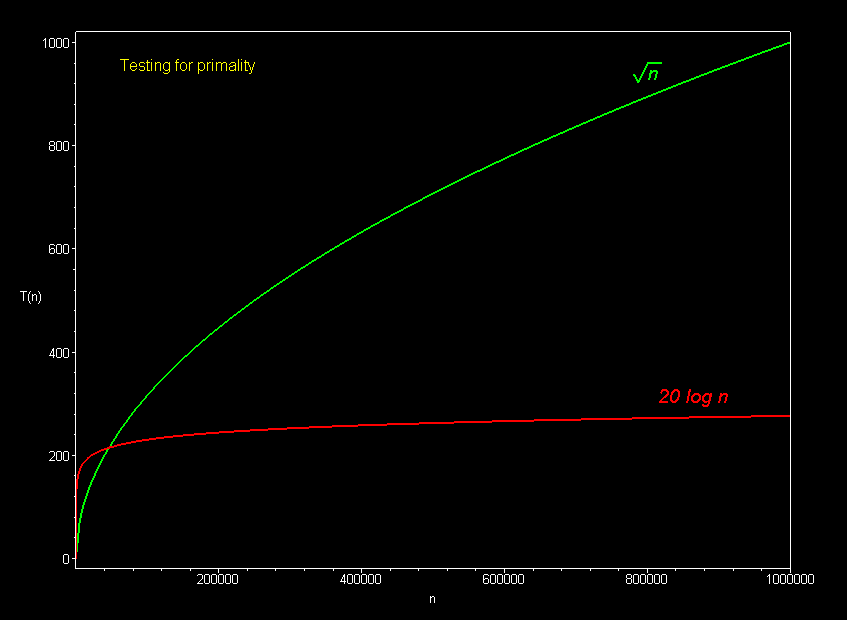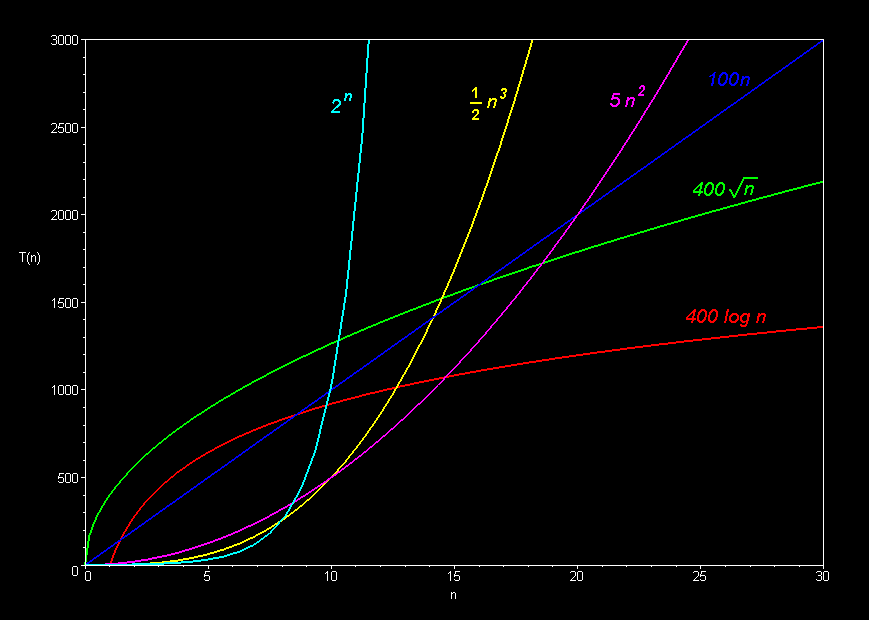
The graph below compares the running times of various
algorithms.

| Algorithm Complexity | Running time T(n)
(measured in seconds on an Apple Delicious computer) |
Maximum problem size given 1000 seconds on an Apple Delicious | Computer Speed x
10
Maximum problem size given 1000 seconds on a Power Delicious (or 10,000 seconds on a classic Delicious) |
| O(n) | 100n | n = 10 | n = 100 (x 10 increase) |
| O(n2) | 5n2 | n = 14 | n = 45 (x 3) |
| O(n3) | ½ n3 | n = 12 | n = 27 (x 2) |
| O(2n) | 2n | n = 10 | n = 13 (x 1.3) |
| O(sqrt n) | 400 sqrt(n) | n = 6 | n = 625 (x 100) |
| O(log n) | 400 log(n) | n = 12 | n = 72 billion (x 6 billion) |
MORAL: Cheaper, faster computers mean bigger problems to solve.
Bigger problems to solve mean efficiency is more
important.
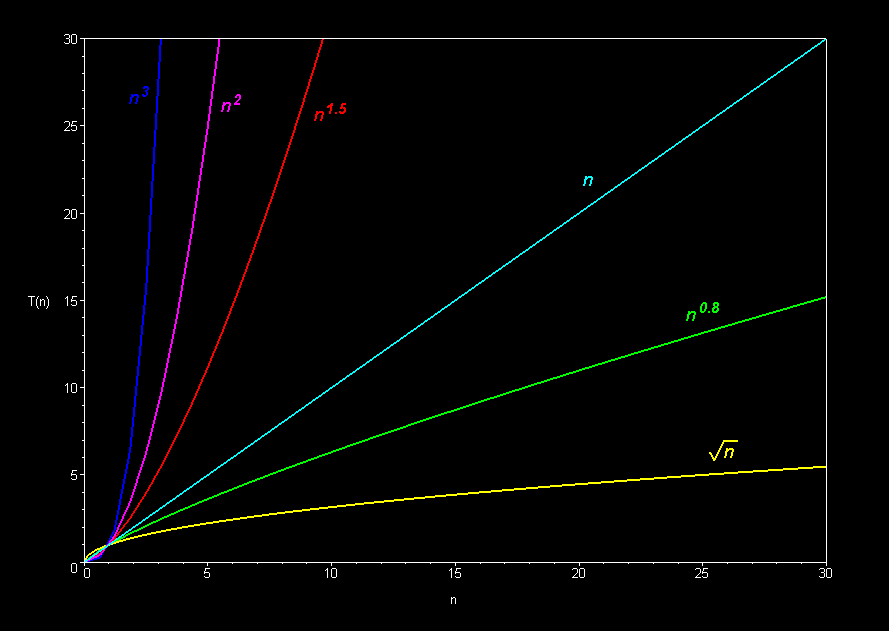
The basic shape of a polynomial function is determined by the highest valued exponent in the polynomial (called the order of the polynomial).
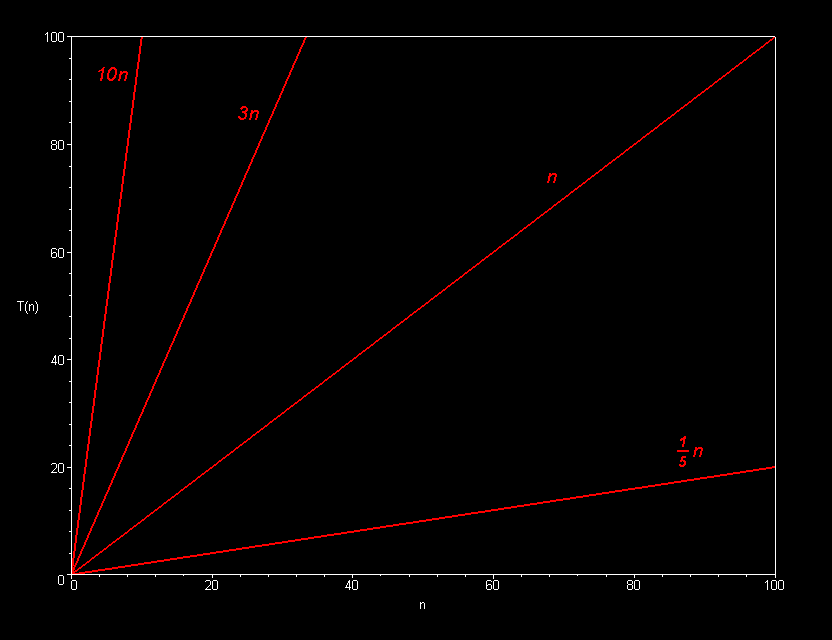
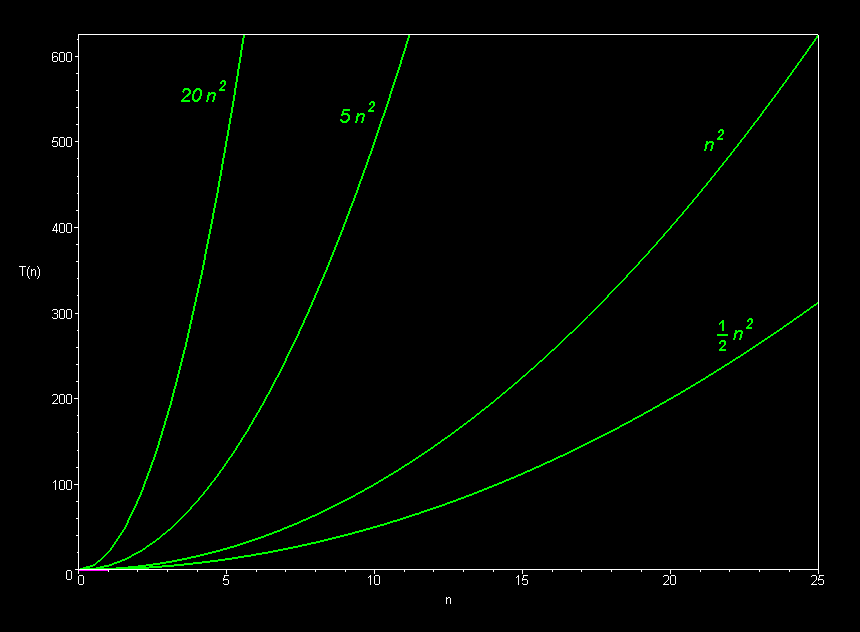
Multiplicative constants do not affect the fundamental
shape of a curve. Only the steepness of the curve is affected.
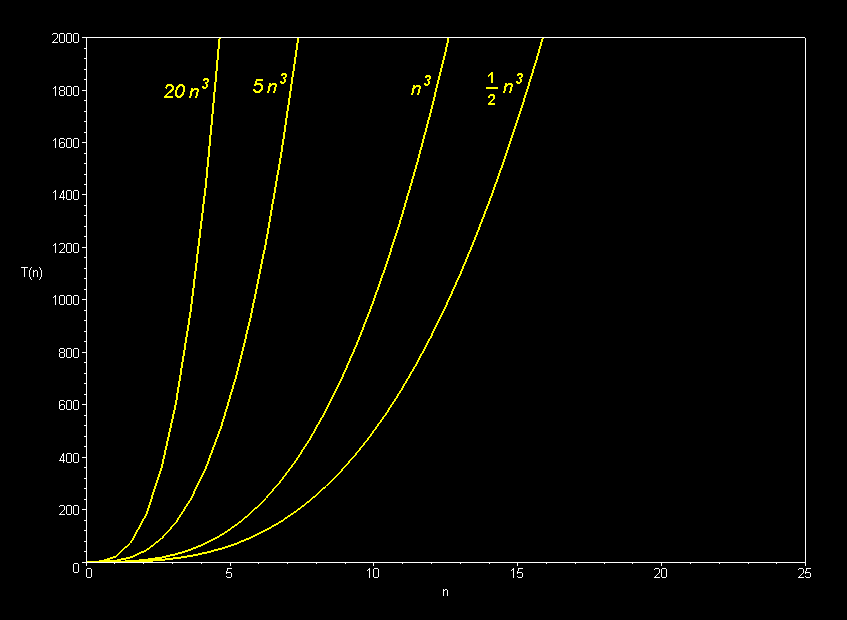
Only the dominant terms of a polynomial matter in the long run. Lower-order terms fade to insignificance as the problem size increases.
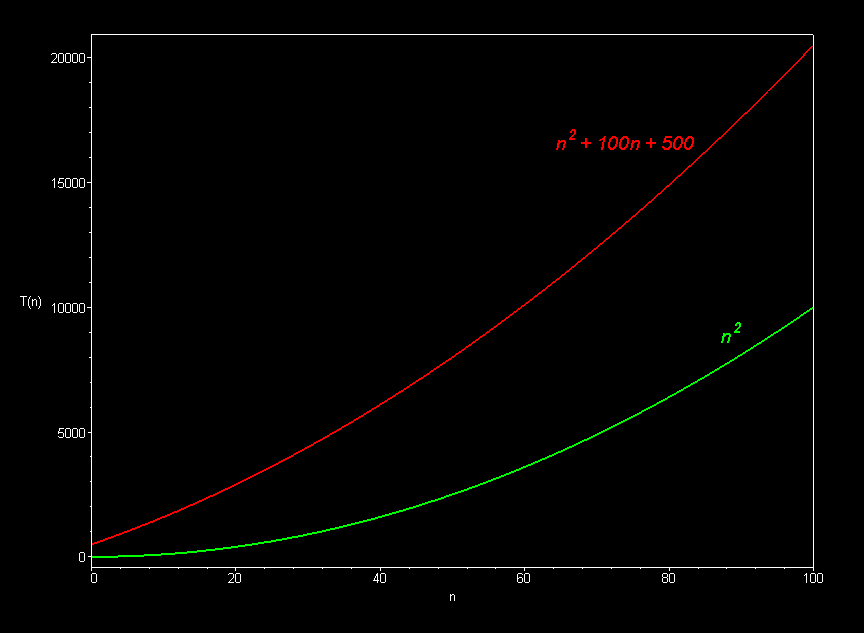
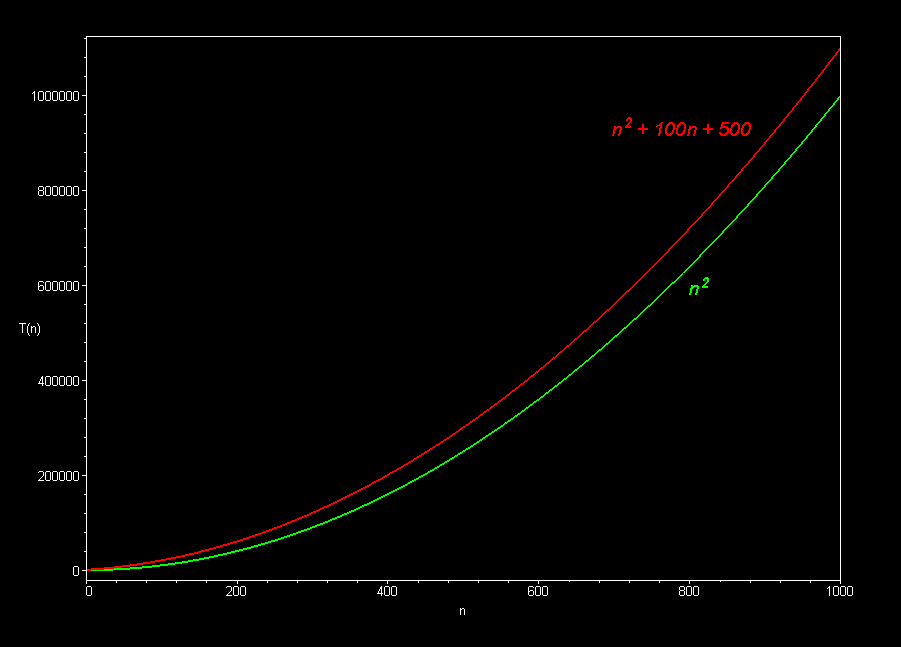
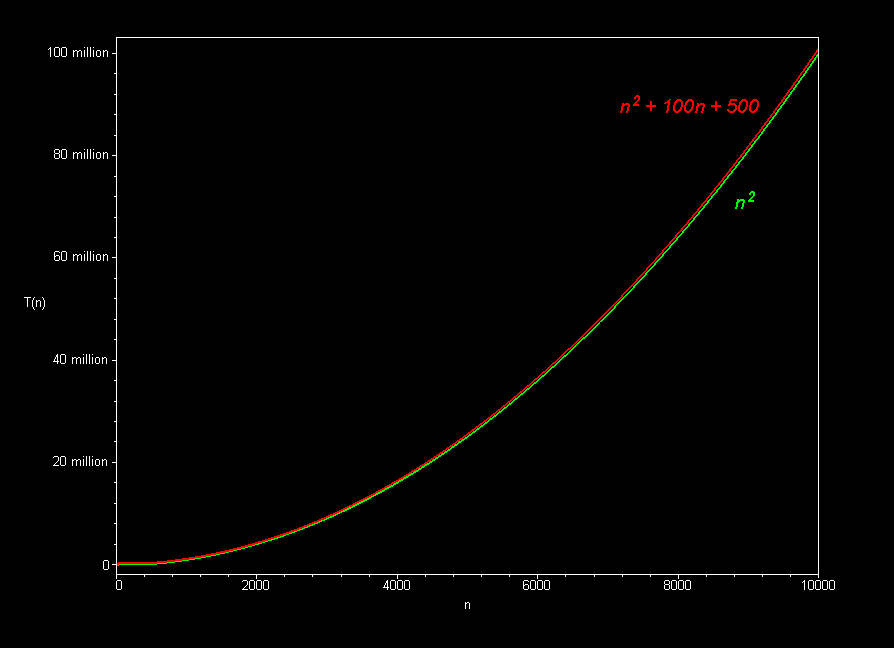
The best sorting algorithms (such as mergesort) run in O(n log n) time. Slower ones (such as bubble sort, selection sort, and insertion sort), take O(n2) time.
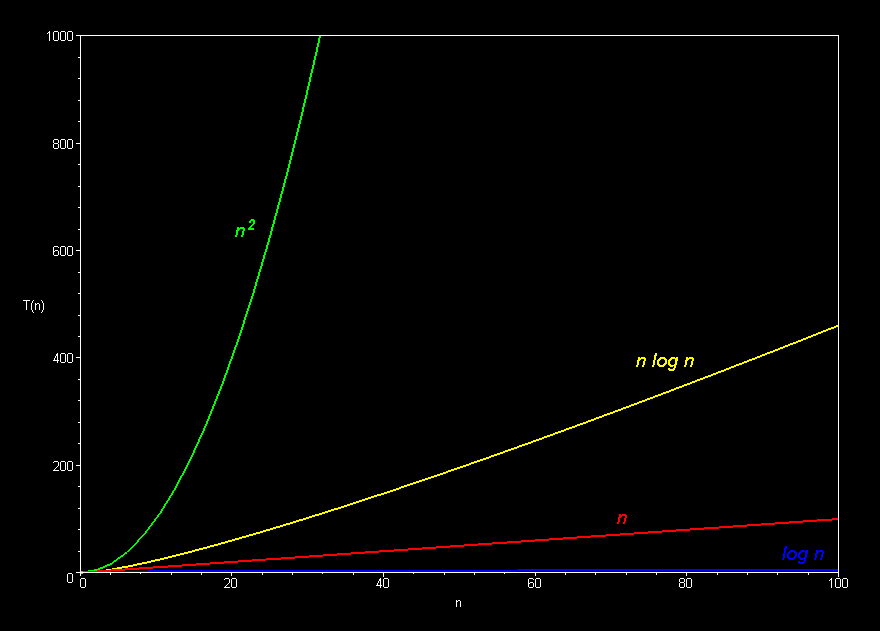
Polynomial curves will always overtake logarithmic curves eventually, when the problem size gets big enough, regardless of the multiplicative constants involved.
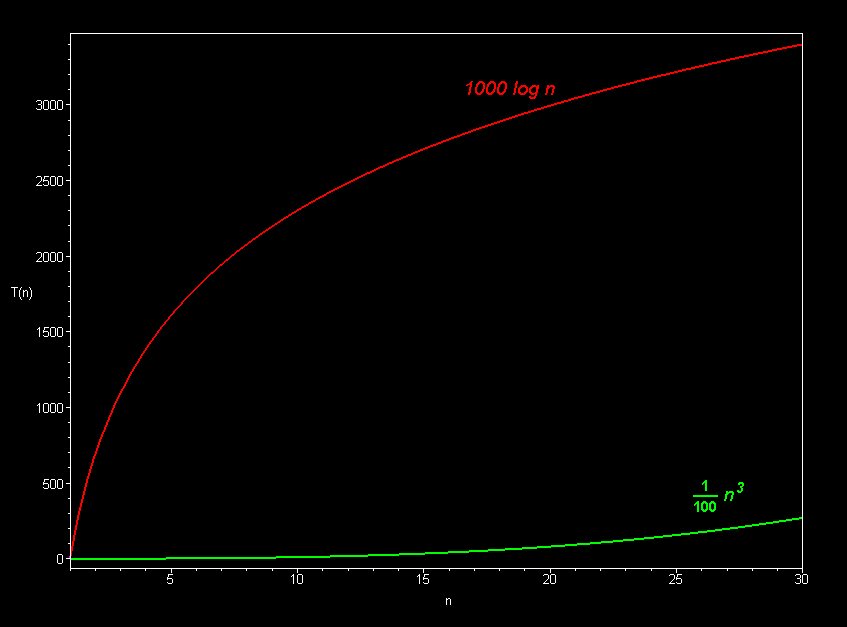
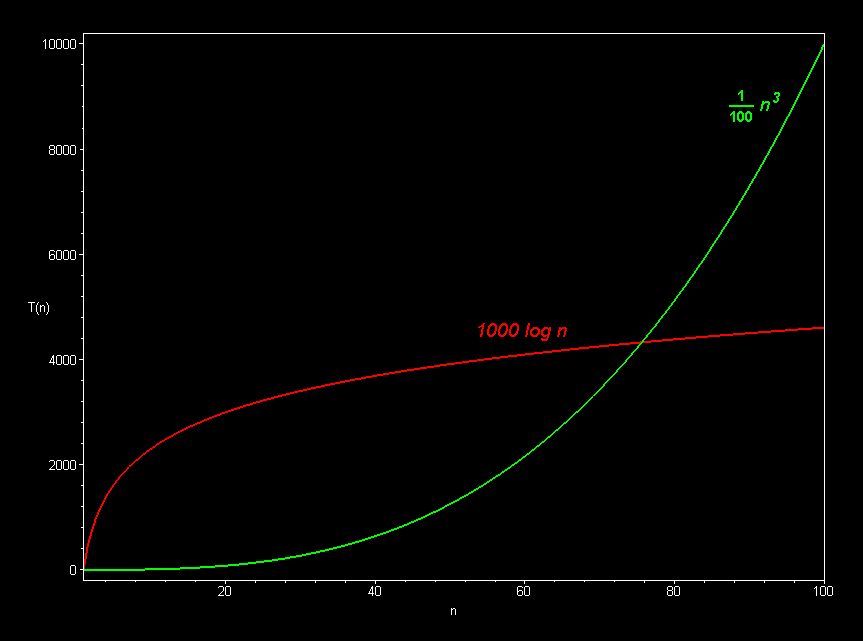
The superiority of the O(log n) Fermat prime test over the O(sqrt n) prime test becomes clear for really big integers.