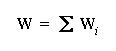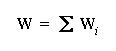CS 152 Assignment 2

Assignment 2 -- The Linear Associator

Due by class time Monday, October 7

Introduction

For our first real experiment in neural modelling let us investigate the linear associator model for associative memory. This model displays many of the virtues of distributed neural models and is easy to implement. It is described in detail in Chapters 6 and 7 of the textbook. A general discussion of the theory behind linear associators can be found on pages 163-168.

You will make use of the programs you developed in the first assignment. Your basic strategy will be to write a program that implements a linear associator and then study it just as you would study any new system. I will make some suggestions for things to look at, but please feel encouraged to try your own ideas. Because many of the qualitative properties displayed by the linear associator are shown by more complex neural models it is worth taking some care with the writeup and experimentation for this assignment.

The essence of this assignment is to show that a generalized Hebb synapse realizes a powerful associative system. In fact, almost all variants of Hebb synapses realize associative systems, one of the things that initially caused most people to believe that they must exist in some form or other in the nervous system given the associative nature of human memory. There is now very good biological evidence for Hebb synapses, probably of several kinds, in the brain.

Your task in this simulation will have several parts.

Part One

You should generate normalized random vectors as test patterns and use them to construct a weight matrix W. A good dimensionality to use at first would be between 50 and 100. You should know how to generate such vectors from Assignment 1. (Interesting simulation question: does it make a difference whether you use elements with normally distributed, uniformly distributed, or random binary values, that is, +1/-1? Obviously the length of the vector makes a difference, but does the distribution of element values? In fact, it makes almost no difference. You might want to verify this on your own, however. A much more difficult question asks: if element values can be -1, 0, or +1, does the fraction of zeros make a difference? This question touches on hard questions about data representation.)

Your job in the simulation is to generate random vectors f and g, compute W, and show that W f gives an output g₀ in the same direction as g. (Actually, with normalized input and learning rate 1, vectors g and g₀ will be equal.) Specifically, compute the cosine between g and g₀. It should be one. Compute the length of g₀. It should be one as well. Generate a new normalized random vector f'. Check to see if it is more or less orthogonal to f by looking at the cosine of the angle between f and f'. Compute W f' and look at the length of this vector. What do you think it should be? What is it?

Part Two

Next, store different numbers of associations f -> g in the memory.

Generate pairs of random vectors f_i-> g_i
Compute the outer product matrices
W_i= g_if_i^T
Form the overall connectivity matrix, W, as the sum of the individual outer product matrices

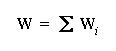
W will change as it accumulates more and more pairs. Constructing truly orthogonal sets of vectors can be done but is not easy except for one trivial case. (What is it?) So trust to high dimensionality to give you approximate orthogonality, which is a more realistic and interesting case in any event. Then test the resulting matrix as follows:

Compute the output for each stored input.
Compare it with what it should be by computing the cosine between the actual output and the true association. Also compute the length of the output vector. Both values should be close to one.
Compute the average cosine and length for the entire set of stored inputs.
Generate a new set of random vectors and compute the matrix product between each of these vectors and the matrix. If our system is to develop any selectivity, we would hope that the output of the system to a new random vector would be small. Compute the length of the outputs for the vectors and compare the lengths to what was stored. Compute the average length. If you feel ambitious, you might plot the "data" collected here in the form of a histogram as you did before.
Repeat for different numbers of stored vectors, and observe how the behavior of the system deteriorates as more and more vectors are stored. For example, if you work with a 50 dimensional system, interesting numbers of stored vectors to look at might range from 1 (should be perfect) to 60 (should be poor) with a few intermediate values.

Part Three

Perform a computational experiment using the system. You only need to do one of the below, or, better yet, think up your own.

Destroy parts of the matrix at random and see how it distorts the output. That is, do an "ablation" experiment. One of the virtues of matrix models is generally felt to be their resistance to noise and damage. Convince yourself that this biologically important property is true. You can use the cosine between pre- and post-ablated outputs as a measure of damage. There are other measures, but this is a reasonable one and it is easy to compute. Question: Would you expect the response of the system to damage to depend on the representation of data in the network? If so, why? Can you give reasons?
Make chains of associations. That is, store vector associations f -> g, g -> h, h -> i, i -> j, etc. Observe how noise increases if we start off with f and cycle output back through the system. This particular demonstration is dramatic when compared to the same thing done using the error correcting learning algorithm we'll study shortly.
If f = g for all pairs of patterns, we have an autoassociative system. (One way to view autoassociation is that it forces the system to develop a particular set of eigenvectors.) Autoassociative systems are described on pages 168-170 of your textbook. This technique has the valuable property that if part of f is put into the system it will regenerate the missing part. This is what is called the reconstructive property of autoassociative memories. Demonstrate this property using your simulation. A good approach might be to look at what happens to the missing (zero) parts of the vector. There is now considerable belief that autoassociative network memories may actually exist in the hippocampus, a cortical structure known to be involved in memory.
Many variants of the simple outer product learning rule are possible. There are indications from biology that small changes in synaptic activities are not learned. This could be implemented quite nicely by simply putting in a modification threshold, so that no modification occurs unless some parameter is above threshold. Possible obvious parameters would be pre-synaptic activity, post-synaptic activity, or their product. You might try a product threshold as the most obvious candidate, and the most in harmony with the outer product rule. This rule would also be easy to implement since it would simply involve checking the outer product matrix for values below threshold and then setting them to zero. (Obviously you will have to check to see how many values are set to zero. If there are too many or too few obvious things will happen.) Check to see what difference setting small values to zero makes in the associative properties of the system. A rule of thumb that one hears occasionally says something like "the largest 25 percent of the connection strengths do almost all the work." Is this true?

Turning in Your Homework

You may use Java, C/C++, MATLAB, Perl, or any other reasonable programming language for this assignment. Your code should be handed in electronically, using the cs152submit (or cs152submitall) command on turing. A file called README.txt that explains clearly how to compile and run your simulation is also required. In addition, please turn in a writeup of your experiments in class. Your writeup should explain as clearly as possible what experiments you did, what results you got, and what you concluded from it all. Think of it as a science lab report.

Based on an assignment by James A. Anderson